Graphing: Slope-Intercept Form by Karen Cameron (best novels in english .TXT) 📖

Getting Started

First, we need to lable our axes.  The y-axis, in blue, is our vertical axis.  The x-axis, in orange, is our horizontal axis.  This means that "y" values move up or down, while "x" values move left or right.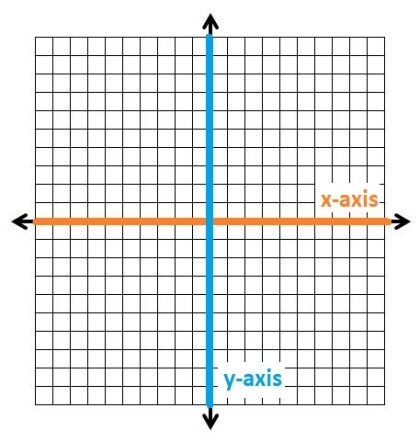

Slope - It's How We Move!

There are 4 types of slope to be aware of.

Positive Slope - The line goes up and to the right.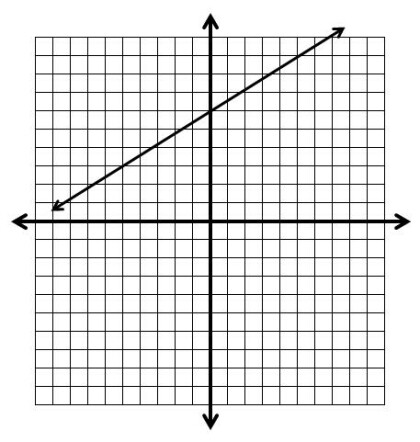

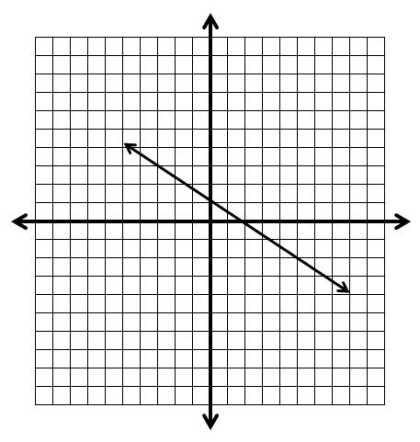
Negative Slope - The line goes down and to the right.

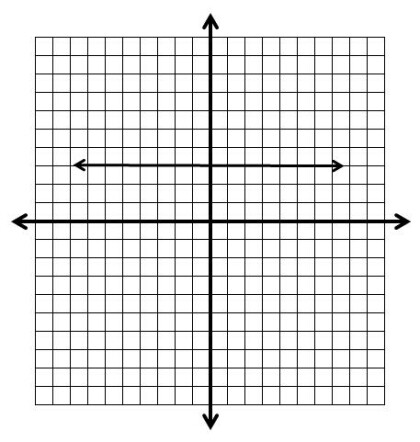
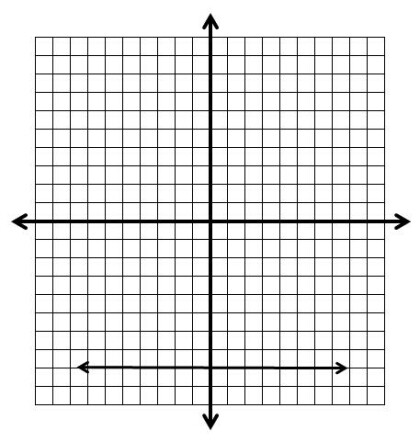
Zero Slope - The line goes straight across.

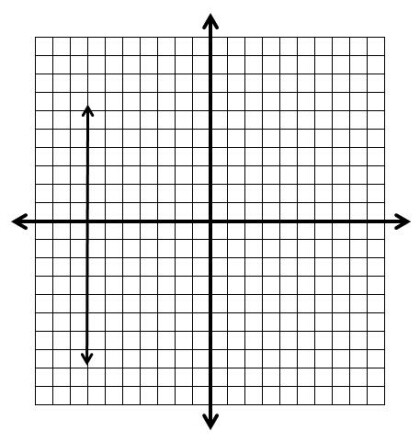
Undefined Slope - Slope is undefined, causing a vertical line.

Slope-Intercept Form

When graphing lines, we typically use SLOPE-INTERCEPT form.

Slope-Intercept form is:  y = mx + b, where m is slope and b is the y-intercept.

To be in slope-intercept form, the equation of the line must begin with a y = .

To graph a line, we need to know where to begin and how to move. 

Our y-intercept is b, this tells us where to begin.  On your graph, you will put a point in this spot.

Our slope is m, this tells us how to move.  From our y-intercept, we move.  We always move up or down and then right.  If the slope is positive, move up and to the right.  If the slope is negative, move down and to the right.

 

 

Learn to Graph

Let's learn how to graph.

Take the equation to the line:  y = 2/3x + 6.  To graph this line, start with the y-intercept.  The y-intercept tells us where to begin, so we will begin on our graph at y = 6.  Since the 6 is positive, move up 6 on the y-axis and put a point.  Now, from this point we need to move.  Our slope is 2/3 (two over three).  So from positive 6, move up 2 (don't put a point), then, over 3 (now put a point).  Now, you have two points on your graph and two points make a line.  So, connect the points, extending your line to the edge of the graph, don't forget arrows on the end because lines go on forever.

 

 

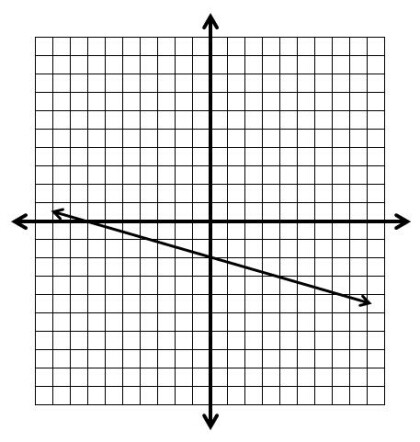
Let's graph another line:  y = -2/3x + 1

First, define m= and b=.  In the equation, m = -2/3 and b = 1.

Recall, b - begin, m - move.  So, begin at positive 1 on the y-axis, then move down 2 and right 3.  Connect the points and you have your line.

Graph:  y = -1/3x - 2

m = -1/3, b = -2

Begin on the y-axis at -2, then move down 1 and right 3.

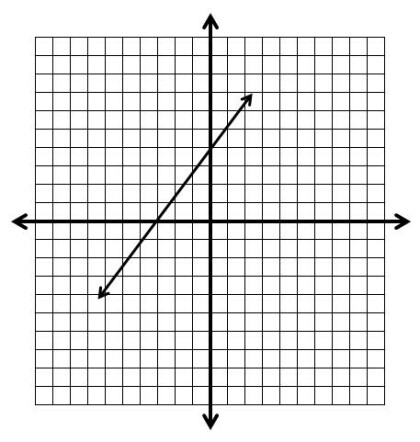
Graph:  y = 4/3x + 4

m = 4/3, b = 4

 

Special Cases

Sometimes, our equations of lines don't look quite right.  They may be missing parts, sort of anyway.

Zero Slope

Zero Slope is just what is sounds like, the slope is 0.

Consider the line, y = 3.  There is no "m" or "x" in the equation, just the "b", the y-intercept.

You could re-write this equation as y = 0x + 3, then you could see that m = 0 and b = 3.  Whenever we have an equation with a y =  some number, we simply move on the y-axis and draw a horizontal line.  This seems counter-intuitive to what we want to do, but really you are marking all the places on the graph where y equals that number.

 

 

 

 

Graph:  y = 3.

Simply move up 3 on the y-axis, plot your point and draw a horizontal line.

 

Graph:  y = -8.

Move down 8 on the y-axis and draw a horizontal line.

 

Undefined Slope

Undefined slope occurs when we have an x= equation.  Essentially we are dividing our slope by zero, causing a vertical line.  Whenever we have an x= equation, we are showing on the graph all the places where x is equal to some number.  We need to move on the x-axis, plot our point and draw a vertical line.  Again, this seems to go against our intuition, but remember in order to see where on the graph x is equal to some number, we must draw a vertical line.

 

 

 

 

 

 

Graph:  x = -7

Move left 7 on the x-axis, plot your point and draw a vertical line.

 

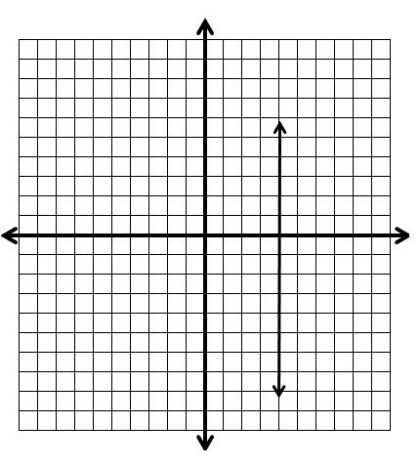
Graph:  x = 4.

Move right 4 on the x-axis, plot your point and draw a vertical line.

Imprint

Text: Karen Cameron
Editing: Karen Cameron
Publication Date: 11-17-2013

All Rights Reserved