Secrets of Mental Math by Arthur Benjamin (namjoon book recommendations TXT) 📖

of lines 1 and 2 on line 3, then the sum of lines 2 and 3 on line 4, and so on as illustrated below.

Finally, have the spectator show you the card. At a glance, you can tell him the sum of all the numbers on the card. For instance, in our example, you could instantly announce that the numbers sum up to 671 faster than the spectator could do using a calculator! As a kicker, hand the spectator a calculator, and ask him to divide the number on line 10 by the number on line 9. In our example, the quotient 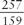= 1.616.… Have the spectator announce the first three digits of the quotient, then turn the card over (where you have already written a prediction). He’ll be surprised to see that you’ve already written the number 1.61!

Why This Trick Works

To perform the quick calculation, you simply multiply the number on line 7 by 11. Here 61 × 11 = 671. The reason this works is illustrated in the table below. If we denote the numbers on lines 1 and 2 by × and y, respectively, then the sum of lines 1 through 10 must be 55x + 88y, which equals 11 times (5x + 8y), that is, eleven times the number on line 7.

As for the prediction, we exploit the fact that for any positive numbers, a, b, c, d, if a/b • c/d, then it can be shown that the fraction you get by “adding fractions badly” (i.e., adding the numerators and adding the denominators) must lie in between the original two fractions. That is,

Thus the quotient of line 10 divided by line 9 (21x + 34y)/(13% + 21y), must lie between

Hence, the ratio must begin with the digits 1.61, as predicted.

In fact, if you continue the leapfrog process indefinitely, the ratio of consecutive terms gets closer and closer to

a number with so many amazingly beautiful and mysterious properties that it is often called the golden ratio.

MAGIC SQUARES

Are you ready for a challenge of a different sort? Below you will find what is called a magic square. There has been much written on magic squares and how to construct them, going back as far as ancient China. Here we describe a way to present magic squares in an entertaining fashion. This is a routine I’ve been doing for years.

I bring out a business card with the following written on the back:

I say, “This is called a magic square. In fact, it’s the smallest magic square you can create, using the numbers one through sixteen. You’ll notice that every row and every column adds to the same number—thirty-four. Now I’ve done such an extensive study on magic squares that I propose to create one for you right before your very eyes.”

I then ask someone from the audience to give me any number larger than 34. Let’s suppose she says 67.

I then bring out another business card and draw a blank 4-by-4 grid, and place the number 67 to the right of it. Next I ask her to point to the squares, one at a time, in any order. As she points to an empty box, I immediately write a number inside it. The end result looks like this:

I continue: “Now with the first magic square, every row and column added to thirty-four. [I usually put the thirty-four card away at this point.] Let’s see how we did with your square.” After checking that each row and column adds up to 67, I say: “But I did not stop there. For you, I decided to go one step further. Notice that both diagonals add up to sixty-seven!” Then I point out that the four squares in the upper left corner sum to 67 (16 + 19 + 22 + 10 = 67), as do the other three four-square corners, the four squares in the middle, and the four corner squares! “They all sum to sixty-seven. But don’t take my word for any of this. Please keep this magic square as a souvenir from me—and check it out for yourself!”

HOW TO CONSTRUCT A MAGIC SQUARE

You can create a magic square that sums to any number by taking advantage of the original magic square that sums to 34. Keep that square within eyeshot while you construct the volunteer’s magic square. As you draw the 4-by-4 grid, mentally perform the calculations of steps 1 and 2:

1. Subtract 34 from the given number (e.g., 67 − 34 = 33).

2. Divide this number by 4 (e.g., 33 ÷ 4 = 8 with a remainder of 1). The quotient is the first “magic” number. The quotient plus the remainder is the second “magic” number. (Here our magic numbers are 8 and 9.)

3. When the volunteer points out a square, inconspicuously look at the 34-square and see what is in the corresponding square. If it is a 13, 14, 15, or 16, add the second number to it (e.g., 9). If not, add the first magic number (e.g., 8).

4. Insert the appropriate number until the magic square is completed.

Note that when the given number is even, but not a multiple of 4, then your first and second magic numbers will be the same, so you’ll have just one magic number to add to the numbers in your 34-square.

Why This Trick Works

The reason this method works is based on the fact that every row, column, diagonal (and more) from the originally displayed magic square sums to 34. Suppose the given number had been 82. Since 82 − 34 = 48 (and 48 ÷ 4 = 12), we would add 12 to each square. Then every group of four that had previously summed to 34 would add to 34 + 48 = 82. See the magic square below.

On the other hand, if the given number were 85, our magic numbers would be 12 and 15, so we would be adding 3 more to the squares showing 13, 14, 15, and 16. Since each row, column, and group of four contains exactly one of these numbers, each group of four would now add to 34 + 48 + 3 = 85 in the following magic square.

As an interesting piece of mathemagical trivia, let me point out another astonishing property of the famous 3-by-3 magic square below.

Not only do the rows, columns, and diagonals add up to 15, but if you treat the rows of the magic square as three-digit numbers, you can verify on your calculator that 4922 + 3572 + 8162 = 2942 + 7532 + 6182. Also, 4382 + 9512 + 2762 = 8342 + 1592 + 6722. If you are curious about why this property happens, you might want to explore my paper Magic “Squares” Indeed! (included in the bibliography).

QUICK CUBE ROOTS

Ask someone to select a two-digit number and keep it secret. Then have him cube the number; that is, multiply it by itself twice (using a calculator). For instance, if the secret number is 68, have the volunteer compute 68 × 68 × 68 = 314,432. Then ask the volunteer to tell you his answer. Once he tells you the cube, 314,432, you can instantly reveal the original secret number, the cube root, 68. How?

To calculate cube roots, you need to learn the cubes from 1 to 10:

Once you have learned these, calculating the cube roots is as easy as p. For instance, with this example problem:

What is the cube root of 314,432?

Seems like a pretty tough one to begin with, but don’t panic, it’s actually quite simple. As usual, we’ll take it one step at a time:

1. Look at the magnitude of the thousands number (the numbers to the left of the comma), 314 in this example.

2. Since 314 lies between 63 = 216 and 73 = 343, the cube root lies in the 60s (since 603 = 216,000 and 703 = 343,000). Hence the first digit of the cube root is 6.

3. To determine the last digit of the cube root, note that only the number 8 has a cube that ends in 2 (83 = 512), so the last digit ends in 8.

Therefore, the cube root of 314,432 is 68. Three simple steps and you’re there. Notice that every digit, 0 through 9, appears once among the last digits of the cubes. (In fact, the last digit of the cube root is equal to the last digit of the cube of the last digit of the cube. Go figure out that one!)

Now you try one for practice:

What is the cube root of 19,683?

1. 19 lies between 8 and 27 (23 and 33).

2. Therefore the cube root is 20-something.

3. The last digit of the problem is 3, which corresponds to 343 = 73, so 7 is the last digit.

The answer is 27.

Notice that our derivation of the last digit will only work if the original number is the cube root of a whole number. For instance, the cube root of 19,684 is 27.0004572 … definitely not 24. That’s why we included this in our mathemagical magic section and not in an earlier chapter. (Besides, the calculation goes so fast, it seems like magic!)

SIMPLIFIED SQUARE ROOTS

Square roots can also be calculated easily if you are given a perfect square. For instance, if someone told you that the square of a two-digit number was 7569, you could immediately tell her that the original number (the square root) is 87. Here’s how.

1. Look at the magnitude of the “hundreds number” (the numbers preceding the last two digits), 75 in this example.

2. Since 75 lies between 82 (8 × 8 = 64) and 92 (9 × 9 = 81), then we know that the square root lies in the 80s. Hence the first digit of the square root is 8. Now there are two numbers whose square ends in 9: 32 = 9 and 72 = 49. So the last digit must be 3 or 7. Hence the square root is either 83 or 87. Which one?

3. Compare the original number with the square of 85 (which we can easily compute as 80 × 90 + 25 = 7225. Since 7569 is larger than 7225, the square root is the larger number, 87.

Let’s do one more example.

What is the square root of 4761?

Since 47 lies between 62 = 36 and 72 = 49, the answer must be in the 60s. Since the last digit of the square is 1, the last digit of the square root must be 1 or 9. Since 4761 is greater than 652 = 42 25, the square root must be 69. As with the previous cube root trick, this method can be applied only when the original number given is a perfect square.

AN “AMAZING” SUM

The following trick was first shown to me by James “the Amazing” Randi, who has used it effectively in his magic. Here, the magician is able to predict the total of four randomly chosen three-digit numbers.

To prepare this trick you will need three sets of nine cards each, and a piece of paper with the number 2247 written down on it and then sealed in an envelope. Next, on each of the three sets of cards do the following:

On Set A write the following numbers, one number on each card:

4286  5771  9083  6518  2396  6860  2909  5546  8174

On Set A write the following numbers:

5792  6881  7547  3299  7187  6557  7097  5288  6548

On Set C write the following numbers:

2708  5435  6812  7343  1286  5237  6470  8234  5129

Select three people in the audience and give each one a set of cards. Have each of your volunteers randomly pick one of the nine cards they hold. Let’s say they choose the numbers 4286, 5792, and 5435. Now, in the sequence, have each one call out one digit from the four-digit number, first person A, then person B, and finally person C. Say they call out the numbers 8, 9, and 5. Write down the numbers 8, 9, and 5 (895) and say, “You must admit that this number was picked entirely at random and could not possibly have been predicted in advance.”

Next, have the