Secrets of Mental Math by Arthur Benjamin (namjoon book recommendations TXT) 📖

in the middle of 801. Our next example illustrates that it sometimes pays to factor the numbers in an order that exploits this situation. Let’s look at two ways of computing 67 × 42:

67 × 42 = 67 × 7 × 6 = 469 × 6 = 2814
67 × 42 = 67 × 6 × 7 = 402 × 7 = 2814

Ordinarily you should factor 42 into 7 × 6, as in the first example, following the rule of using the larger factor first. But the problem is easier to solve if you factor 42 into 6 × 7 because it creates a number with a 0 in the center, which is easier to multiply. I call such numbers friendly products.

Look for the friendly product in the problem done two ways below:

43 × 56 = 43 × 8 × 7 = 344 × 7 = 2408
43 × 56 = 43 × 7 × 8 = 301 × 8 = 2408

Did you think the second way was easier?

When using the factoring method, it pays to find friendly products whenever you can. The following list should help. I don’t expect you to memorize it so much as to familiarize yourself with it. With practice you will be able to nose out friendly products more often, and the list will become more meaningful.

Numbers with Friendly Products

12: 12 × 9= 108

13: 13 × 8= 104

15: 15 × 7= 105

17: 17 × 6= 102

18: 18 × 6 = 108

21: 21 × 5 = 105

23: 23 × 9 = 207

25: 25 × 4 = 100, 25 × 8 = 200

26: 26 × 4 = 104, 26 × 8 = 208

27: 27 × 4 = 108

29: 29 × 7 = 203

34: 34 × 3 = 102, 34 × 6 = 204, 34 × 9 = 306

35: 35 × 3 = 105

36: 36 × 3 = 108

38: 38 × 8 = 304

41: 41 × 5 = 205

43: 43 × 7 = 301

44: 44 × 7 = 308

45: 45 × 9 = 405

51:51 × 2 = 102, 51 × 4 = 204, 51 × 6 = 306, 51 × 8 = 408

52: 52 × 2 = 104, 52 × 4 = 208

53: 53 × 2 = 106

54: 54 × 2 = 108

56: 56 × 9 = 504

61: 61 × 5 = 305

63: 63 × 8 = 504

67: 67 × 3 = 201, 67 × 6 = 402, 67 × 9 = 603

68: 68 × 3 = 204, 68 × 6 = 408

69: 69 × 3 = 207

72: 72 × 7 = 504

76: 76 × 4 = 304, 76 × 8 = 608

77: 77 × 4 = 308

78: 78 × 9 = 702

81: 81 × 5 = 405

84: 84 × 6 = 504

86: 86 × 7 = 802

88: 88 × 8 = 704

89: 89 × 9 = 801

Previously in this chapter you learned how easy it is to multiply numbers by 11. It usually pays to use the factoring method when one of the numbers is a multiple of 11, as in the examples below:

52 × 33 = 52 × 11 × 3 = 572 × 3 = 1716
83 × 66 = 83 × 11 × 6 = 913 × 6 = 5478

APPROACHING MULTIPLICATION CREATIVELY

I mentioned at the beginning of the chapter that multiplication problems are fun because they can be solved any number of ways. Now that you know what I mean, let’s apply all three methods explained in this chapter to a single problem, 73 × 49. We’ll begin by using the addition method:

Now try the subtraction method:

Note that the last two digits of the subtraction could be obtained by adding 50 + (complement of 73) = 50 + 27 = 77 or by simply taking the complement of (73 − 50) = complement of 23 = 77.

Finally, try the factoring method:

73 × 49 = 73 × 7 × 7 = 511 × 7 = 3577

Congratulations! You have mastered 2-by-2 multiplication and now have all the basic skills you need to be a fast mental calculator. All you need to become a lightning calculator is more practice!

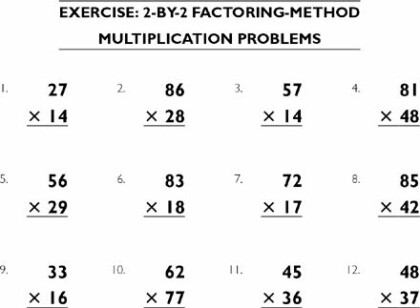
EXERCISE: 2–BY–2 GENERAL MULTIPLICATION—ANYTHING GOES!

Many of the following exercises can be solved by more than one method. Try computing them in as many ways as you can think of, then check your answers and computations at the back of the book. Our answers suggest various ways the problem can be mathemagically solved, starting with what I think is the easiest method.

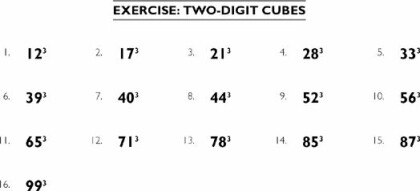
The following 2-by-2s occur as subproblems to problems appearing later when we do 3-by-2s, 3-by-3s, and 5-by-5s. You can do these problems now for practice, and refer back to them when they are used in the larger problems.

THREE-DIGIT SQUARES

Squaring three-digit numbers is an impressive feat of mental prestidigitation. Just as you square two-digit numbers by rounding up or down to the nearest multiple of 10, to square three-digit numbers, you round up or down to the nearest multiple of 100. Take 193:

By rounding up to 200 and down to 186, you’ve transformed a 3-by-3 multiplication problem into a far simpler 3-by-1 problem. After all, 200 × 186 is just 2 × 186 = 372 with two zeros attached. Almost done! Now all you have to add is 72 = 49 to arrive at 37,249.

Now try squaring 706:

Rounding down by 6 to 700 requires you to round up by 6 to 712. Since 712 × 7 = 4984 (a simple 3-by-1 problem), 712 × 700 = 498,400. After adding 62 = 36, you arrive at 498,436.

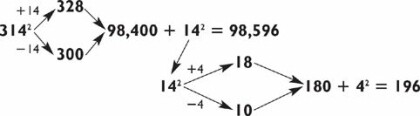
These last problems are not terribly hard because there is no real addition involved. Moreover, you know the answers to 62 and 72 by heart. Squaring a number that’s farther away from a multiple of 100 is a tougher proposition. Try your hand at 3142:

For this three-digit square, go down 14 to 300 and up 14 to 328, then multiply 328 × 3 = 984. Tack on two 0s to arrive at 98,400. Then add the square of 14. If 142 = 196 comes to you in a flash (through memory or calculation), you’re in good shape. Just add 98,400 + 196 to arrive at 98,596. If you need time to compute 142, repeat the number 98,400 to yourself a few times before you go on. (Otherwise you might compute 142 = 196 and forget what number to add it to.)

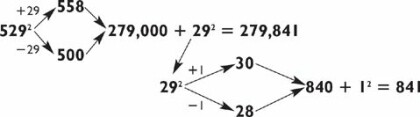
The farther away you get from a multiple of 100, the more difficult squaring a three-digit number becomes. Try 5292:

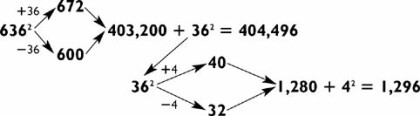
If you have an audience you want to impress, you can say 279,000 out loud before you compute 292. But this will not work for every problem. For instance, try squaring 636:

Now your brain is really working, right? The key here is to repeat 403,200 to yourself several times. Then square 36 to get 1,296 in the usual way. The hard part comes in adding 1,296 to 403,200. Do it one digit at a time, left to right, to arrive at your answer of 404,496. Take my word that as you become more familiar with two-digit squares, these three-digit problems get easier.

Here’s an even tougher problem, 8632:

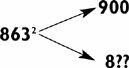
The first problem is deciding what numbers to multiply together. Clearly one of the numbers will be 900, and the other number will be in the 800s. But what number? You can compute it two ways:

1. The hard way: the difference between 863 and 900 is 37 (the complement of 63). Subtract 37 from 863 to arrive at 826.

2. The easy way: double the number 63 to get 126, and take the last two digits to give you 826.

Here’s why the easy way works. Because both numbers are the same distance from 863, their sum must be twice 863, or 1726. One of your numbers is 900, so the other must be 826.

You then compute the problem like this:

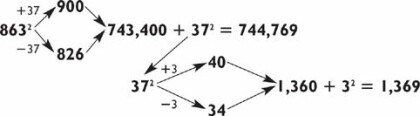
If you find it impossible to remember 743,400 after squaring 37, fear not. In a later chapter, you will learn a memory system that will make remembering such numbers much easier.

Try your hand at squaring 359, the hardest problem yet:

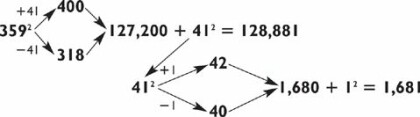
To obtain 318, either subtract 41 (the complement of 59) from 359, or multiply 2 × 59 = 118 and use the last two digits. Next multiply 400 × 318 = 127,200. Adding 412, or 1,681, gives you 128,881. Whew! They don’t get much harder than that! If you got it right the first time, take a bow!

Let’s finish this section with a big problem that is easy to do, 9872:

What’s Behind Door Number 1?

The mathematical chestnut of 1991 that got everyone hopping mad was an article in Parade magazine by Marilyn vos Savant, the woman listed by the Guinness Book of World Records as having the world’s highest IQ. The paradox has come to be known as the Monty Hall problem, and it goes like this.

You are a contestant on Let’s Make a Deal. Monty Hall allows you to pick one of three doors; behind one of these doors is the big prize, behind the other two are goats. You pick Door Number 2. But before Monty reveals the prize of your choice, he shows you what you didn’t pick behind Door Number 3. It’s a goat. Now, in his tantalizing way, Monty gives you another choice. Do you want to stick with Door Number 2, or do you want to risk a chance to see what’s behind Door Number 1? What should you do? Assuming that Monty is only going to reveal where the big prize is not, he will always open one of the consolation doors. This leaves two doors, one with the big prize and the other with another consolation. The odds are now 50–50 for your choice, right?

Wrong! The odds that you chose correctly the first time remain 1 in 3. The probability that the big prize is behind the other door increases to 2 in 3 because the probability must add to 1.

Thus, by switching doors, you double the odds of winning! (The problem assumes that Monty will always give a player the option to switch, that he will always reveal a nonwinning door, and that when your first pick is correct he will choose a nonwinning door at random.) Think of playing the game with ten doors and after your pick he reveals eight other nonwinning doors. Here, your instincts would probably tell you to switch. People confuse this problem for a variant: if Monty Hall does not know where the grand prize is, and reveals Door Number 3, which happens to contain a goat (though it might have contained the prize), then Door Number 1 has a 50 percent chance of being correct. This result is so counterintuitive that Marilyn vos Savant received piles of letters, many from scientists and even mathematicians, telling her she shouldn’t write about math. They were all wrong.

CUBING

We end this chapter with a new method for cubing two-digit numbers. (Recall that the cube of a number is that number multiplied by itself twice. For example, 5 cubed—denoted 53—is equal to 5 × 5 × 5 = 125.) As you will see, this is not much harder than multiplying two-digit numbers. The method is based on the algebraic observation that

A3 = (A – d)A(A + d) + d2A

where d is any number. Just like with squaring two-digit numbers, I choose d to be the distance to the nearest multiple of ten. For example, when squaring 13, we let d = 3, resulting in:

133 = (10 × 13 × 16) + (32 × 13)

Since 13 × 16 = 13 × 4 × 4 = 52 × 4 = 208, and 9 × 13 = 117, we have

133 = 2080 + 117 = 2197

How about the cube of 35? Letting d = 5, we get

353 = (30 × 35 × 40) + (52 × 35)

Since 30 × 35 × 40 = 30 × 1,400 = 42,000 and 35 × 5 × 5 = 175 × 5 =